11 Buckling in Columns

Columns’ behavior in structural systems can be studied regarding their geometrical properties, loading type, and construction material. Following our discussion from the previous chapters, we will discuss the effect of columns’ geometrical properties on potential failure modes of columns in buildings. Columns can be categorized into two contrasting groups of long and short columns. When the ratio of the effective length of a column to its least lateral dimension is equal to or less than 12, the column is considered short. In general, short columns fail by crushing.

f_c=[latex]\frac{P}{A}≤[/latex] F_c

Where:

f_c = Actual compressive stress

A = Cross-sectional area of column (in²)

P = Load on the column

F_c = Allowable compressive stress per codes

Long or slender columns are those whose ratio of effective length to its least lateral dimension is more than 12. A long column fails due to buckling where the structural component under compression bows quickly. the buckling phenomenon in ling columns is due to the inevitable eccentricities in loading and the likelihood of irregularities in materials’ resistance to compression.  Long columns generally fail by buckling before reaching their limit of compressive stress. Accordingly, the load-carrying capacity of long columns is less than short columns.

Video 11-1: Demonstration of buckling in long elements in compression (https://www.youtube.com/watch?v=KjgOGw6SqIA&t=2s)

In 1757, a mathematician called Leonhard Euler derived a formula that gives the maximum axial load that a long slender column can carry without buckling. The Euler equation is given below:

F=[latex]\frac{π^2IE}{KL^2}[/latex]

Where:

F = Maximum allowable or critical compressive stress

A = Cross-sectional area (in²)

E = Modulus of elasticity of the column material (psi)

K = Stiffness (curvature mode) factor; The K factor can be derived from the following table.

L = Column length between ends (inches)

Table 11-1: K factor in columns (source: column effect length, 2006, https://commons.wikimedia.org/wiki/File:ColumnEffectiveLength.png)

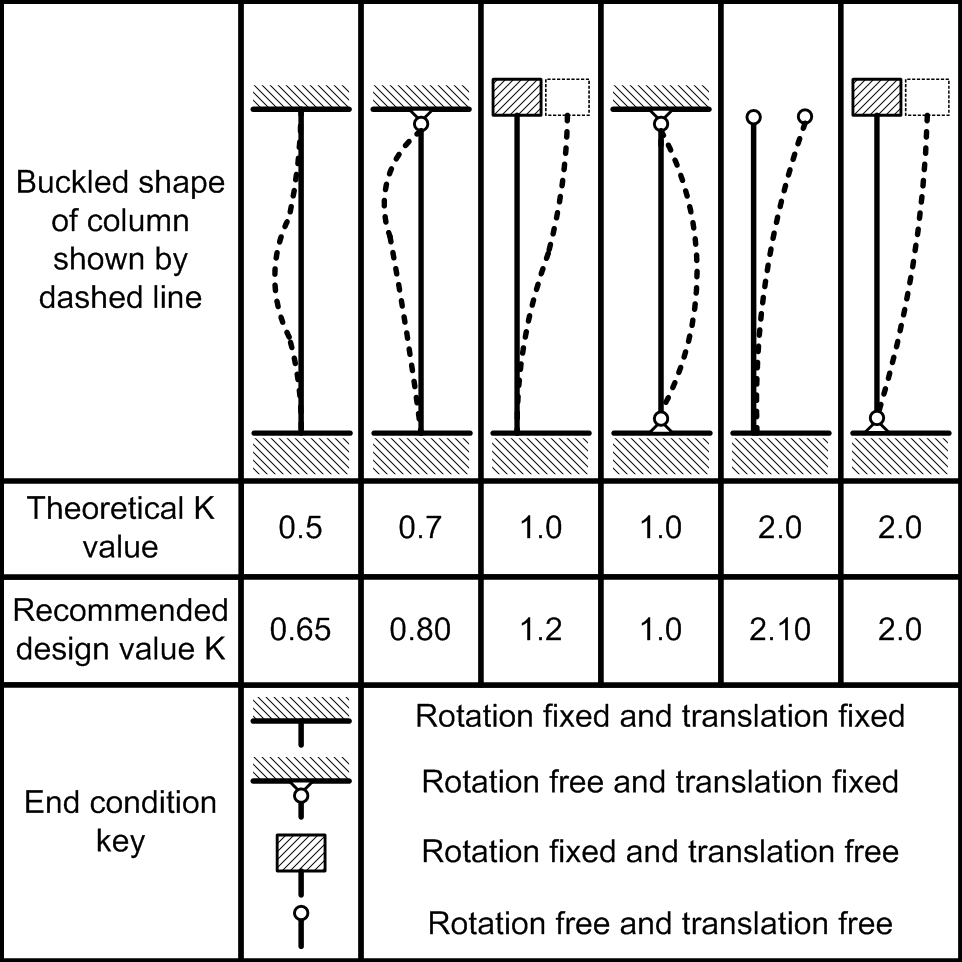
According to Leonhard Euler, the load under which a compressive element (such as a column) may buckle depends on its slenderness. The slenderness of a compressive element depends on:

• The length of the element
• The cross-sectional area
• 2nd moment of area
• Young’s modulus of the element’s material
• The support condition (K factor).

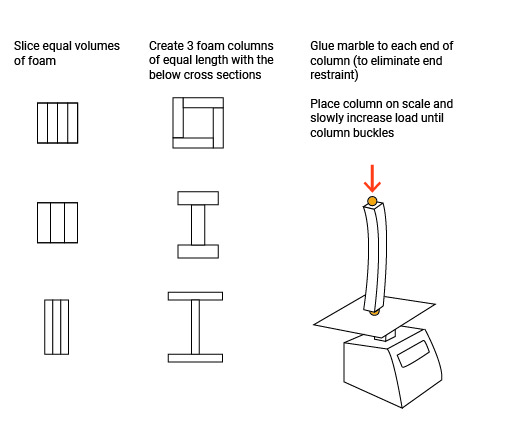
• Which of the following cross-sectional shapes will give a more stable column? Why?

Figure 11-2: The effect of a column’s cross-sectional shape on its stiffness