Main Body
Consonance and Dissonance
We have already been using intervals for some time, but the only measuring rulers we have been using are the Whole and Half steps. Counting large pitch distances–intervals–with this method is very inefficient, prone to errors, and not how musicians talk about them. In addition, building chords is not done with W and H steps–you have to understand the rest of the intervals.
One concept that people generally judge music on is how “pleasant” sounding it is; that’s a subjective word, for sure, but it evokes a widespread psycho-perceptual concept of a favorable musical experience. It’s not that we always want music to sound pleasant; in fact, we enjoy the contrast of certain “harsher” elements of music being introduced. These subjective words are narrowed down to more precise terms with consonance and dissonance. Now that we are discussing intervals, we need to have a more accurate sense of how notes sound together.
Listen to this song by Pentatonix:
Regardless of whether you like their style (or not), most would agree that their harmony–the blending of notes together—has an overall pleasing effect. Musicians call this consonant harmony.
Consider this piece, by Pat Metheny:
Again, some listeners might find this pleasing as a matter of style, but, generally, most people would find this rough sounding or displeasing, which musicians call dissonant.
There are two aspects to consonance and dissonance: acoustic/psychological and stylistic/historical. Certain intervals, due to the physiological nature of our hearing (literally, the cochlea and nerve cells in our ear) sound “rough” or “smooth,” and are generally accepted across cultures as “harsh” or “pleasing.” Within a certain style or time period, context can affect these judgments. This is reflected in the names used for Western musical intervals; for sure, this is only one perspective on these, but this is the musical system we are operating in. Finally, these descriptions below refer to these intervals primarily as harmonic intervals–when the pitches sound at the same time; how they are used melodically are somewhat different, discussed more below.
Lecture Video, Consonance and Dissonance:
Interval Numbers
The first step in naming the interval is to find the distance between the notes as they are written on the staff. Beginning with the first note, count all lines and spaces until, and including the second note. This gives you the number for the interval.
How to count interval numbers.
 1b)
1b) 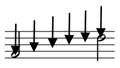 2a)
2a)  2b)
2b) 
The Number is simply counting up total lines and spaces–1a and 1b. Notice that a clef is not needed. With a clef–2a and 2b–interval number is also the same as counting pitch letter names.
The interval from 3rd line to 4th line (1a), from B to D (2a) is a “third”. The interval from the bottom space to 4th line (1b), from A to F (2b) is a “sixth”. Note that at this stage the key signature, clef, and accidentals do not matter at all. Interval number is only categorizing the pitch letter names (lines/spaces).
See the Appendix for Simple and Compound Interval definitions.
Lecture Video – Interval Numbers:
Concept Check
Example 5-1, 5-2: Name the intervals; write a note that will give the named interval – follow the direction.

Interval Qualities
With interval number, the actual distance in half-steps has not mattered, as explained in the video: G up to D is a 5th, as is G# up to D, but the quality would change due to the accidental changing the number of half steps. More examples: a third made up of three half-steps sounds different from a third made up of four half-steps; a fifth made up of seven half-steps sounds very different from one of only six half-steps (see and hear the Noteflight example below). In the second step of identifying an interval, clef, key signature, and accidentals become important: this is known as identifying the quality of the interval.
To illustrate this, look and listen through the example below. The pitches A to C natural and A to C sharp are both thirds, but A to C sharp is a larger interval (4 hs versus only 3 hs), with a different sound. The difference between the intervals A to E natural and A to E flat (both 5ths) is also noticeable to the ear. Be sure to listen to this example.
Look & Listen!
Before we continue defining the intervals qualities, let’s define the categories of qualities.
Lecture Video: Interval Categories:
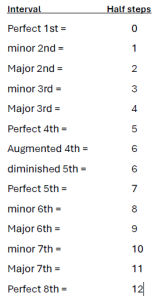
Recapping the video: again, here are the five descriptive interval names:
- Perfect – doesn’t mean without flaw; refers to the consonance of this category and mathematical simplicity of the ratios.
- Major – literally, “bigger”.
- Minor – literally, “smaller”.
- Diminished – make even smaller.
- Augmented – make even bigger.
As you can tell by these definitions, these are all relative terms to some starting point. The chart below shows the relative size of each category.
Interval numbers are separated into two groups (based, historically, on the simplicity of their mathematical ratios).
Number and Interval Qualities.
There are two basic categories, grouped by interval number: prime (1), 4th, 5th, and 8th intervals can only be diminished, perfect, or augmented; all 2nd, 3rd, 6th, and 7th intervals can only be diminished, minor, major, or augmented. Interval number categories have limited “crossover.” You can’t have a Major 5th, nor will you have a Perfect 7th. Only Diminished and Augmented apply to both categories.

The double arrows represent ONE half step difference between each adjacent quality. As the chart states, to the left is smaller, meaning the pitches are closer together (picture them on the piano); to the right is larger, meaning the pitches are farther apart.
So let’s define the intervals, specifically, as they occur through an octave. Each interval below is defined by how many half steps make it up. Count these on the piano.
- Take two pitches a certain interval number apart that you’d like to create, say a minor 6th. For example, create a m6 above D.
- D to B = a 6th interval number. NOTE: you must do the number/pitch category first or you can make an enharmonic mistake.
- A m6 needs 8 half steps. D to B is 9 half steps, so we need to make it Bb to get to 8.
- Remember, always think of the number category first. In this example, if you only counted 8 half steps up from D, you would likely end on A#. That’s correct if you wanted an augmented 5th – D to A#, but you have to make the number category correct first (D to B), and then adjust the quality.
Knowing the definition of an interval by how many half steps is fine to start with, but isn’t practical in the long run, so we introduce other methods below. This method, though, along with the categories chart above, can help you figure out any interval – it’s just not very fast.
Now, look and listen to the examples below; notice that you can make an interval quality smaller or larger by changing the top note or the bottom note. Why? Because you are making either the top note or the bottom note move closer or farther from the other note by half steps; regardless of which one you change, the distance between them is changing. Notice also the importance of the enharmonic spelling of the notes: the number is determined by the pitch name (lines/spaces)–not the enharmonic equivalent on the piano. Interval names are about how it is spelled on the page! [Notice the double sharp on the bottom d3 interval–that’s enharmonic to an A natural on the keyboard.]
Look & Listen!
Lecture Video: Changing Interval Qualities:
Calculating Intervals Faster
In order to classify intervals more quickly and accurately, we need a starting point, a reference point, to quickly figure out what they are. This is very practical to understand: memorize a starting point for interval qualities, and then make adjustments for ones that are not memorized. As noted above, counting half steps works, but is slow and can have errors with larger intervals (it’s easy to make a mistake while counting 10 or 11 half steps).
White Key Intervals
One better method is to use the white keys on the piano as your starting point. This basically gives you a chart that gives the interval qualities for all of the white keys on the piano. Every interval you calculate starts with the closest white key. Once you know this quality, then modify with accidentals to get to the quality you need.
WK-Intervals-Method-Charts.pdf
Let’s use the same example: create a minor 6th above D. Locate the 6ths intervals and find D to B, which will show as a M6, then change the B to Bb for the minor quality.
Video Lecture: White Key Intervals
Intervals Through Scales
Concept Check
Example 5-3: Give the complete name for each interval: number and quality. These intervals are presented melodically–one note after another, rather than harmonically. To find them on the chart, go from the lower pitch to the higher, regardless of which note comes first.

Concept Check
Example 5-4: Complete the interval.

Concept Check
Example 5-5: Complete the interval.
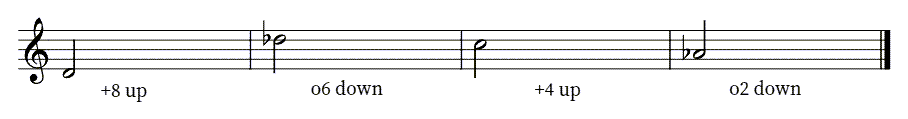
Inverting Intervals
Knowing how to invert intervals is important for two reasons: 1) it can be used as a shortcut to identify and build intervals; 2) to understand how inversion works with chords (coming up next). To invert any interval, simply imagine that one of the notes has moved one octave, so that the higher note has become the lower and vice-versa (this works in both directions!).
Look & Listen!
While inverting, the numbers and the qualities maintain certain pattern, as shown here:
Patterns for Interval Inversion. The numbers always add up to 9, and the Quality patterns are easy to remember: P stays P, the “M’s” swap, and then the “extremes” swap–the largest A and the smallest d.

Lecture Video, Interval Inversion:
Concept Check
Example 5-6: What are the inversions of the following intervals?
- Perfect fifth
- Diminished fifth
- Major seventh
- Minor sixth
Introduction to Chords
Chords form the basis of harmony in most music that we perform and listen to. Fundamentally, harmony is playing two or more pitches at the same time; an interval is a simple form of harmony. Usually, harmony is two or three voices singing melodies together, or one singer with a piano or guitar accompaniment. These can create different textures (patterns of multiple voices and/or instruments), but generically they make up harmony.
Since the concept of harmony is somewhat free-flowing–multiple voices (or one voice and an instrument) that may or may not sing at exactly the same time–how does a chord fit into this concept? A chord is a convenient way to take a collection of notes, for example, 3-4 notes, and put them into a group with one label name, like a C Major chord, or an Eb Dominant 7th chord, or a Dsus4 chord, etc. Depending on the texture, these groups of notes are more or less easy to see and hear. Look at this Bach Chorale hymn; here, the chord groupings are easy to see as a vertical stack of notes (blue boxes); each vertical group of notes constitutes a 3-note chord being sung by 4 voices (notice that one pitch is always doubled in each chord):
Chords as vertical grouping. Each vetical grouping notes, arranged by color, represents a chord, even though each horizontal line represents four different melody lines.
In this Debussy excerpt, from Première Arabesque, the notes of the chords are spread out–arpeggiated–but are still considered a chord.
Chords as arpeggiated grouping. In this excerpt, the chords are “spread out” horizontally, but can still be “grouped” into a chord structure.
Now, consider this orchestra score: https://youtu.be/lLxJcC8S4HU?t=309. This demonstrates the usefulness of chords when you realize that all of those instruments and notes can mostly be boiled down to 3 or 4-note chords. In fact, harmony in Western music is based mostly on triads: three-note chords.
There are 12 lines of music in this example; notice the heavy black vertical line on the left of the score–that groups all 12 staves together into a system. As the video progresses, note that they put two systems (of 12 staves each) per page. Again, the point here is that those 12 staves of notes can be distilled down to 3 and 4 note chords at any given point in the music.
Lecture Video, Chords Introduction:
Chord Structure and Position
Triads in Root Position
Triads are the most common type of chord used in our styles of music. We need to clarify two terms: Triad means a 3-note chord. Tertian refers to the interval used to build the chord–the 3rd. Don’t confuse the two separate uses of three.
Parts of a chord.

The basic triad is built using stacked 3rd intervals, and when they are stacked only in 3rds, this is called Root Position (other arrangements covered below). The named parts of the chord—Root, 3rd, 5th—are important to understand and remember. The 3rd of the chord is written a third higher than the root, and the 5th of the chord is written a fifth higher than the root.
Root Position Takeaway
One of the interesting things about chords is that they maintain their identity, even when they are broken apart and rearranged (remember the Debussy above). It does not matter how far the higher notes are from the lowest note, or how many of each note there are (doubles at different octaves or on different instruments, like in the orchestra score video example above); what matters is which note is lowest, as you can see below. ALL five examples of this G major chord are in root position, because G, the root (in red), is the lowest sounding pitch; even when the other notes are rearranged in various ways above the Root, that does not affect the position label.
Look & Listen!
Concept Check
Example 6-1: Write a triad in root position using each root given; no accidentals are needed here:

Lecture Video, Triads–Basic Structure – this video just looks at the basic definition of a chord and the name of each part: Root, 3rd, 5th. The quality of chords (similar to intervals) will be discussed soon.
First and Second Inversions
You may have wondered why it’s important to determine Root Position by which note is the lowest. Why not the highest? The reason, as with most practices in art and music, is partly history and partly physics. The physics part is a bit beyond this class, but this video discusses the Harmonic Series, which is related to why the Bass is considered the fundamental voice within a chord.
A Little Science
The connection he makes between the harmonic series and the pentatonic scale has some validity, but is not the sole explanation for how the crowd sang the scale; there are cultural reasons as well. 1) many cultures share the pentatonic scale; 2) even the pentatonic scale is decided on by musical choices; 3) the harmonic series is a choice as well – strings, air columns, shaped pieces of metal (bells, vibraphones) all use this, but the inharmonic series could also be a choice. For example, traditional church bells are tuned slightly inharmonically (less simple mathematical ratios), as a choice, and harmonically tuned bells are an experimental choice.
It’s easy to understand how the melody line is the most important one in music; what’s less well-known is the importance of the Bass voice (we use the word “bass” generically a lot in music – it’s the lowest sounding instrument or voice). You may have an idea already about the importance of the bass player in a rock band and a jazz big band – that is somewhat dependent on the time period and style. Much of modern pop music uses electronic bass instead; however, the importance of the bass is still there. That is actually a very old concept in music history.
Composers and performers in much of western culture developed a particular style and texture that favored the highest and the lowest voices, which primarily has to do with the fact that they are easiest to hear when there are multiple voices. Additional voices filled out the harmony, but the Bass and the Soprano (again, these names are used generically for the lowest and highest voices or instruments) came to be considered the essential framework for the harmony. In the 17th century, the Bass voice became the primary structural voice, the foundation, for establishing the flow of the chord progression of a piece. This texture and technique was called Figured Bass (this notation was in use well into the 18th century). We won’t study figured bass in this course, but it’s good to know about if you study music further, especially if you are interested in more historic styles.
Lecture Video: Chord Inversions
Once you’ve established which pitch is the Root, we can then begin to rearrange chords into different positions. If the third of the chord is the lowest note, the chord is in first inversion. If the fifth of the chord is the lowest note, the chord is in second inversion.
Chord Inversions
All three of the triads are C major (as C is the root in all three, marked red), but which note is in the bass voice determines the position: Root or an Inversion. With the 3rd of the chord in the bass, it is 1st inversion; 5th of the chord in the bass is 2nd inversion. 5-3, 6-3, and 6-4 are alternate names for inversion, based on something called Figured Bass (covered in Theory I, Music 1A@LBCC), an older system still used to a degree today, but mostly important for understanding/performing historical music scores. For this course, it gives a shorthand way of understanding the interval construction of chord positions when they are compressed as close as possible on one staff.
Here is another example with a G chord, showing more variations.
Key Takeaways
Inverting a chord–changing the bass position note–has several musical uses, which we will discuss later. It also creates a new “sound” or “effect” on the chord: inverted chords generally sound less “stable,” so it’s a nice variety (listen to the above examples).
It’s important to remember that a chord maintains its identity no matter how it is arranged: if the Root is C, that doesn’t change regardless of where the root is placed in the voicing of the music. That holds true for the other parts of the chord as well–the 3rd and the 5th remain the same pitches that they were no matter where they show up. Also, doubling notes–having 2 or more copies in different octaves also does not change the identity of the chord. In summary, to find root position:
- Remove any doubled notes.
- The Root is determined by arranging the notes so that they stack in 3rd intervals–this can only work one way (remove any doubled notes and compress the notes close together); the root is the lowest pitch.
- The Bass note determines which position is being used–Root (Rt) or an Inversion (3rd or 5th of chord)
Finding root position.
In both cases, after getting rid of the doubled notes, the only way to rearrange the notes into stacked 3rds is to begin on G, whether you right them in the treble or bass clef.

“Voicing” is how the notes are arranged in the music: how many notes are doubled, tripled, etc.; how spaced apart the notes are, etc.. Root Position rearranges the notes in 3rd intervals to determine which note is the Root. The first inversion example above has multiples of each note – that’s a voicing choice that doesn’t change the name of the chord or the inversion; the same applies to the 2nd inversion example.
Concept Check
Example 6-2: Rewrite each chord in root position and name the original position of the chord.

Naming Triad Qualities
Chords are named according to the root and the interval qualities between the notes when the chord is in root position. Play these four different G chords to hear how they differ, and note how the intervals inside each chord change.
Look & Listen!
These are all G chords, but they are four different qualities of G chords. The interval qualities between the notes are different, so the overall chord qualities sound very different. We will next explore how these chords are built.
Lecture Video: Triad Qualities
Defining Major and Minor Chords
The most commonly used triads are major chords and minor chords.
- All major chords and minor chords have an interval of a perfect fifth between the root and the fifth of the chord.
A perfect fifth can be divided into a M3 plus a m3. If the interval between the root and the third of the chord is the M3 (the “bottom” 3rd), then the triad is a major chord. If the interval between the root and the third of the chord is the m3, then the triad is a minor chord. Both chords derive their name from the quality of the bottom 3rd. Listen closely to a major triad and a minor triad in the Triad Chord Qualities Noteflight file above.
Arrangement of the 5th and 3rds in Major and Minor Triads. Both major and minor triads have P5 (red) from root to 5th. The 3rds have a swapped pattern: major triad has M3 on bottom – root to 3rd (purple) and a m3 on top – 3rd to 5th (green). The minor triad has the opposite 3rds pattern. The major triad is named by the M3 on bottom and the minor by the m3 on bottom.

Additional examples of Major and Minor Triads. All 5ths are perfect; M3 and m3 from root determine the triad quality.
Concept Check
Example 6-3: Build major and minor triads: 1) Build a P5 above each root; 2) build a M3 above the first four; 3) build a m3 above the last three.

Defining Augmented and Diminished Chords
Because they don’t contain a P5, augmented and diminished chords have an unsettled feeling and are normally used sparingly. An augmented chord is built from two M3’s, which adds up to an augmented fifth, which is where it derives its name. A diminished chord is built from two m3’s, which add up to a diminished fifth, which is where it derives its name.
Diminished and augmented examples. All diminished traids have a d5 (o5), all augmented triads have an A5 (+5).
Be careful when spelling diminished and augmented chords to avoid enharmonic spelling mistakes: make sure that when the chord is in root position, it is spelled with two 3rds, as with all triads. See below for examples of problems:
Changing the spelling of any note in a chord can significantly alter chord’s name and structure.
You can put the chord in a different position or add more of the same-named notes at other octaves without changing the name of the chord. But changing the note names or adding different-named notes will change the name of the chord.
Concept Check
Example 6-4: Build diminished and augmented triads: 1) Build an o5 above the root of the first four; 2) build an +5 above the root of the last three; 3) build a m3 above the root of the first four; 4) build a M3 above the root of the last three.

Concept Check
Example 6-5: Identify the Root, Quality, and Inversion of these triads that are not necessarily in root position. Rewrite them in root position first: stack up in 3rds by letter names (only write each pitch once for those that are doubled).

Next-Level Chord Knowledge
Recognizing and spelling chords with the information above works well to start. If you want to become more proficient, though, you need to learn your chords in keys, which is how musicians think about chords. Similar to using the major scale as a starting point for intervals, the same approach works for chords. However, the challenge is that it takes time and practice to memorize and be comfortable with the key signatures and scales. Learning these on an instrument is the best way to do this, typically on a keyboard. The method we are using works well for beginning students who don’t have prior performance experience.
- Triad qualities in any major scale – the quality of the chords spelled on each scale degree remains the same for every major scale.
- We’ll expand on this concept in Chapter 7.
Chord Labels, Inversions, and Lead sheet Symbols
So far, we’ve only labeled the chords by naming the root and the quality, e.g., B minor. Musicians need a less cumbersome method of labeling chords. This is practical for composers, arrangers, and performers (especially those using many chords, like pianists and guitarists), who need to be able to talk to each other about the chords that they are reading, writing, and playing.
Chord manuals, fingering charts, chord diagrams, and notes written out on a staff are all very useful, especially if the composer wants a very particular sound (called a “voicing”) on a chord. In many cases, though, all you really need to know are the name of the chord, your major scales and minor scales, a few rules, and you can figure out the notes in any chord. If you know all your scales (always a good thing to know for so many reasons), you can find all the intervals from the root using scales. If you plan to take the Jazz Theory course, being proficient at these skills will be extremely helpful.
Chord Symbols and Lead sheets
Some instrumentalists, such as guitarists and pianists, are often expected to be able to play a named chord, or an accompaniment based on that chord, without seeing the notes written out in staff notation. In such cases, a chord symbol above the staff tells the performer what chord should be used as an accompaniment to the melody until the next symbol appears. This is called “lead sheet” notation. It’s used in conjunction with “fake books” and “charts,” which have to do with a player showing up to a gig, and being able to play along (“fake it”) with other musicians on “sight”. The idea is that you are given the “lead” part—the melody—and then the player comes up with their own accompaniment (depending on the instrument), based on the chord symbols, to go along with the melody, as below.
Chord Lead sheet Symbols
Excerpt from the song “Popular,” from the musical Wicked.

From the sample page @ https://www.musicnotes.com/ – one of many sites that sell lead sheet music scores.
Here are the basic chord symbols used for lead sheet, below. The example above has a couple chords that are covered in later courses (such as “add9”.)
Summary chart of the basic lead sheet symbols for triads.

From Robert Hutchinson’s OER text: https://musictheory.pugetsound.edu/
Another example of lead sheet, from Beyonce’s “Sandcastles,” which also includes the guitar fretboard symbol and a notated piano accompaniment. The fretboard symbols are just a basic guide for a beginning guitarist; the guitarist would need to improvise or imitate the original. The pianist could read the given version, improvise their own, based on the lead sheet, or do a combination of both.

From sample page @ musicnotes.com
In popular music, it’s relatively straightforward how lead sheet symbols are used, as covered in the video below. Some of the symbols, like in the examples above, above would need some more study, but it’s easy to find many guides for these online. Once you know the basics from a course like this, transferring and expanding your chord knowledge just takes some regular practice.
In jazz music, the chord system is quite a bit more extensive and fairly complicated, and beyond this course. In addition, which symbols are used has changed slightly over time. In reality, the best way to understand jazz chord theory and symbols is to take a jazz theory course (Music 29@LBCC) as well as play with other jazz musicians (Music 43 – Jazz Improvisation; Music 57AD – Jazz Combos and Music 23AD – Jazz Choir). Within historical music theory, Roman Numeral symbols are also used (Ch. 7 in this course and further in Music 1A).
This figure is just for illustration but gives a brief sense of how chord symbols can get more complicated in more advanced music. If your goal is mostly focused on songbooks, then you won’t need to worry about most of these – the simple symbols discussed above will suffice.
Additional lead sheet symbols. Most of these are beyond use in this course, and are shown only for illustration.

Lecture Video: Lead sheet Symbols (Lead sheets ends at 2:06; roman numerals, covered starting at 2:07, will be discussed in Ch. 7.)
Lead sheet Symbols and Inversions
Lead sheet music scores communicate inversions with a slash (/) and another pitch letter to state which pitch should be in the bass. For example, the following examples show lead sheet above the staff, where it is typically written:
X/Y, where X always equals the chord root and quality; Y always equals the bass pitch – a single pitch – the lowest sounding note.
Lead sheet symbols with inversions.

Various lead sheet symbols in context.
A final example shows a typical songbook lead sheet with a variety of chord types, including several inversions, circled in green. The bass note, which creates the inversion, is also circled in green. Note for the Eb/G and the last Ab/C chords, the inversion is, again, caused by the bass note – not the higher octave of the same pitch circled in red.

From virtualsheetmusic.com sample page, Shenandoah, Cohen & Smith.
Voicing and Texture
How the notes of a chord move from one chord to another chord is called voice leading. How you place notes inside a given chord is the voicing. This is closely related to the texture of the music: the three notes of one chord voiced on a guitar, versus a piano, versus a choir, versus an orchestra will create very different textures. For this class, we will look at only one texture: basic keyboard.
Keyboard Texture and Voice leading
Here, the chords have been voiced in all root position, which means each chord “jumps” to the next, with the root always on the bottom and the 3rd and 5th only stacked above—somewhat interesting, but not very sophisticated sounding.
Look & Listen
Keyboard texture actually needs two components:
- Put the complete chord in the treble clef, as shown above—this lets the keyboard player “voice” the chord with only their right hand.
- Combine this with a bass “line” in the bass clef (creating a grand staff), which the keyboardist plays with their left hand—this “thickens” the texture for a fuller sound. This also allows for a more complete use of inversion.
Here is a complete keyboard texture:
Look & Listen
Some key points:
- Version A: the bass clef has all of the roots, shown in red. The Treble clef is the same as the previous example. This still sounds very “blocky,” and adding the bass voice thickens the texture, but doesn’t add more varied movement.
- Version B: the treble clef now shows how the three lines of pitches move more smoothly; they move as little as possible as the notes of one chord move to the next. This is done by:
- a) keeping common tones shared between chords;
- b) moving other notes to the next closest note. The roots are still shown in red, but it is not always the bottom note.
- The Bass clef still shows the roots, so the overall texture is still in root position. REMEMBER: inversion is not determined by the bottom note of the treble clef chord, it is determined by the BASS clef note.
- Version C: the bass line has been modified with inversions, shown by the lead sheet and the bass clef notes in black; red still show roots. This is the most interesting texture as the bass line creates another interesting line itself, but also the inversions affect the overall sound.
Keyboard texture provides an easy way for someone to accompany a singer (or instrumental soloist) by creating a simple, yet clear, background texture of the harmony. By voicing the chords mostly in the right hand (treble clef), the complete harmony is easy to play with one hand. By adding the bass line in the bass clef, the acoustics of the lower note create a richer texture and also allow for a clear inversion voice to create a more interesting texture.
What we are covering here is the simplest version of keyboard texture, but is still quite useful. Building on this would be typical songbooks you can find for popular music of all kinds. If you were interested in learning more about it, you could take Music 51A@LBCC, our beginning piano course.

