Main Body
Consonance and Dissonance, Interval Numbers
We have already been using intervals for some time, but the only measuring rulers we have been using are the Whole and Half steps. Counting large pitch distances–intervals–with this method is very inefficient, prone to errors, and not how musicians talk about them. In addition, building chords (Ch. 6) is not done with W and H steps–you have to understand full intervals.
While this course is more of a technical approach to music, the real goal is to have a better understanding of the aesthetics of music. One concept that people generally judge music on is how “pleasant” sounding it is; that’s a subjective word, for sure, but it evokes a widespread psycho-perceptual concept of a favorable musical experience. It’s not that we always want music to sound pleasant; in fact, we enjoy the contrast of certain “harsher” elements of music being introduced. These subjective words are narrowed down to more precise terms with consonance and dissonance. Now that we are discussing intervals, we need to have a more accurate sense of how notes sound together.
Listen to this song by Pentatonix:
Regardless of whether you like their style (or not), most would agree that their harmony–the blending of notes together—has an overall pleasing effect. Musicians call this consonant harmony.
Consider this piece, by Pat Metheny:
Again, some listeners might find this pleasing as a matter of style, but, generally, most people would find this rough sounding or displeasing, which musicians call dissonant.
There are two aspects to consonance and dissonance: acoustic/psychological and stylistic/historical. Certain intervals, due to the physiological nature of our hearing (literally, the cochlea and nerve cells in our ear) sound “rough” or “smooth,” and are generally accepted across cultures as “harsh” or “pleasing.” Within a certain style or time period, context can affect these judgments. This is reflected in the names used for Western musical intervals; for sure, this is only one perspective on these, but this is the musical system we are operating in. Finally, these descriptions below refer to these intervals primarily as harmonic intervals–when the pitches sound at the same time; how they are used melodically are somewhat different, discussed more below.
Naming Intervals
The first step in naming the interval is to find the distance between the notes as they are written on the staff. Beginning with the first note, count all lines and spaces until, and including the second note. This gives you the number for the interval.
How to count interval numbers.
 1b)
1b) 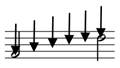 2a)
2a)  2b)
2b) 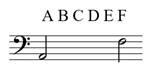
The Number is simply counting up total lines and spaces–1a and 1b. Notice that a clef is not needed. With a clef–2a and 2b–interval number is also the same as counting pitch class letter names.
The interval from 3rd line to 4th line (1a), from B to D (2a) is a “third”. The interval from the bottom space to 4th line (1b), from A to F (2b) is a “sixth”. Note that at this stage the key signature, clef, and accidentals do not matter at all. Interval number is only categorizing the pitch classes, i.e., letter names (lines/spaces).
Interval numbers are also classified by two larger categories: Simple intervals are one octave or smaller.
Look & Listen!
Compound intervals are larger than an octave. You simply keep counting, as you can see from the examples below. From E up to the F an octave higher, E to E would be 8, so F is 9, etc. To convert a compound interval to simple or vice versa, simply add or subtract seven–not eight. If you add/subtract 8, then you are double-counting the octave pitch in your calculation. Prove this to yourself by counting the examples below, and then subtracting 7 from the compound interval. If you move the higher note down an octave, it will match the simple interval.
Look & Listen!
Concept Check
Example 5-1, 5-2: Name the intervals; write a note that will give the named interval – follow the direction.

Classifying Intervals
So far, the actual distance, in half-steps, between the two notes has not mattered. But a third made up of three half-steps sounds different from a third made up of four half-steps. And a fifth made up of seven half-steps sounds very different from one of only six half-steps. In the second step of identifying an interval, clef, key signature, and accidentals become important: this is known as identifying the quality of the interval.
Look & Listen!
The pitches A to C natural and A to C sharp are both thirds, but A to C sharp is a larger interval, with a different sound. The difference between the intervals A to E natural and A to E flat is even more noticeable. Be sure to listen to this example.
While using half steps is adequate to identify the precise differences between intervals of the same number, as mentioned before, using them is inefficient and not practical. Therefore, we have another method, but first, let’s talk about the quality categories.
Interval Quality Categories
Interval qualities can be one of the following, and are put into two separate groups:
Interval Categories by Number and Interval Qualities.

There are two basic categories, grouped by interval number: all prime (1), 4th, 5th, and 8th intervals can only be diminished, perfect, or augmented; all 2nd, 3rd, 6th, and 7th intervals can only be diminished, minor, major, or augmented. Interval number categories have limited “crossover.” You can’t have a Major 5th, nor will you have a Perfect 7th. Only Diminished and Augmented apply to both categories.
Interval Quality Abbreviations
Major: Maj, M Examples: Maj 7th, M7
Minor: Min, m Examples: Min 3rd, m3
Augmented: Aug, A, + Examples: Aug 6th, A6, +6
The double arrows represent ONE halfstep difference between each adjacent quality. As the chart states, to the left is smaller, meaning the pitches are closer together (think about this on the piano to help picture it); to the right is larger, meaning the pitches farther apart.
Look and listen to the examples below; notice that you can make an interval quality smaller or larger by changing the top note or the bottom note. Why? Because you are making either the top note or the bottom note move closer or farther from the other note; regardless, the distance between them is changing. Notice also the importance of the enharmonic spelling of the notes: the number is determined by the pitch name (lines/spaces)–not the enharmonic equivalent on the piano. Interval names are about how it is spelled on the page! [Notice the double sharp on the bottom d3 interval–that’s enharmonic to an A natural on the keyboard.] Enharmonic intervals will be explained in more detail below.
Look & Listen!
History Note
Why do these two category groups (1, 4, 5, 8 and 2, 3, 6, 7) exist? It relates to the discussion of consonance and dissonance. The short answer is that that is how they were classified in music history, and those names have “stuck.” The slightly longer reason has to do with the acoustic and mathematical properties of the intervals: the perfect 1, 4, 5, 8 have simple mathematical ratios (string lengths), respectively: 1:1, 4:3, 3:2, 2:1; whereas 2, 3, 6, 7 have more complex ratios: 9:8, 5:4, 5:3, 15:8. There’s much more to this all, but not needed here.
In order to classify intervals more quickly and accurately, we need a starting point, a reference point, to quickly figure out what they are. This is very important to understand: memorize a starting point for interval qualities, and then make adjustments for ones that are not memorized.
Pitch Class Interval Method
This method uses the white keys on the piano, or the generic pitch-class intervals, i.e., no accidentals to start with.
Look & Listen!
Pitch Class Interval Method ChartPitch Class Interval Method Chart
Resource
Hey! You are going to want to print these charts, like right now. Exactly, stop everything, download and print this document asap: WK Intervals Method Charts
At the very least, have it available in another window to refer to.
Press the play button in the Noteflight version and listen through the entire chart.
Key points for the Pitch Class Interval Chart:
- Number Groups:
- 2nds and 7ths will sound dissonant. Remember, this isn’t a negative judgment–it’s just an acoustic observation that will help classify various musical sounds aurally–and make it easier to hear the difference.
- 3rds and 6ths will sound consonant.
- 4ths and 5ths will sound consonant, but kind of “different”. We don’t use these intervals by themselves much in the past several hundred years (seriously!), so they sound a bit odd or old-fashioned to our ears. I like to describe them as somewhat “hollow” sounding (that will make more sense when we study chords).
- Primes (1) and Octaves (8) are not shown, because they are easy–all of them are Perfect when they have no accidentals, or matched accidentals.
- Blue Intervals:
- You might notice that within each number group, the blue-colored intervals sound different from the rest–they have a different quality (one half step different) from the others in the group.
- Don’t worry if you don’t hear the differences! You will notice it most easily inside the 4th and 5th groups–the F-B and B-F pairs. It takes musicians quite a bit of time and practice to hear these interval differences (not our primary goal in this class). The goal here is to point out the distinction.
- Qualities:
- The qualities for each number group, and the blue distinctions, are listed above each group. Refer to the Category chart above to remember the quality name and difference in half steps.
- Bl. = “blue”; m = minor, M = major; Aug. = augmented (a superscript + sign is also used for Aug.); Dim. = diminished (a superscript o sign is also used for Dim.)
The power of this chart is:
- Understand that the blue intervals–their quality difference–are relatively few within each group. This makes them easier to memorize.
- Realize that for each number group, the remaining intervals are all the same quality. You now have a starting point for a given interval number and quality, and then you modify it using the Category/Quality Chart above.
Shortcuts to remember:
- MAP (Matched Accidental Principal): the starting quality of any interval number remains the same when modified by the same accidental, i.e., if D up to B is a Major 6th, then Db up to Bb is also a M6, because the distance between has not changed.
- 2nds—E-F and B-C are the only HS on the white keys, and they are the only HS in the 2nds!
- 3rds—the ones starting on C, F, G are Major, all others minor.
- 4ths—all are Perfect, except one pair of notes, F and B.
- 5ths—all are Perfect, except one pair of notes, B and F.
- 6ths—the ones starting on E, A, B are minor.
- 7ths—the exact opposite of the 2nd’s—all minor, except the F-E and C-B are Major. Notice that F-E / C-B are the same pitch pairs as the 2nds!
Identifying an interval.
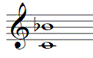
This interval is a 7th, so I find C to B (natural!) on the 7th part of the chart and see that it is Major, and then decrease the interval quality from Major to minor, by using Figure 5-5, on p. 3, to account for the HS change of the flat. Answer: m7.
Here’s another example, but now building the interval.
Building an interval.
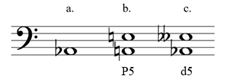
How to build a Diminished 5th, built on an Ab:
a.–We are given Ab.
b.–On the chart, A to E is P5, but so is Ab-Eb (MAP, same accidentals).
c.–Lower the Eb to Ebb for a d5.
Concept Check
Example 5-3: Give the complete name for each interval: number and quality. These intervals are presented melodically–one note after another, rather than harmonically. To find them on the chart, go from the lower pitch to the higher, regardless of which note comes first.

Concept Check
Example 5-4: Complete the interval.

Concept Check
Example 5-5: Complete the interval.
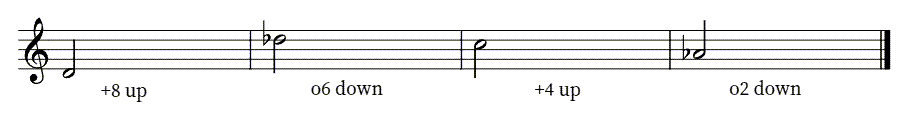
Enharmonic Intervals
The diminished fifth and augmented fourth sound the same on the keyboard. Why? Both are six half-steps, or three whole tones, so another term for this interval is a tritone. In Western Music, this unique interval, which cannot be spelled as a major, minor, or perfect interval, is considered unusually dissonant and unstable (tending to want to resolve to another interval). It’s also unique because it splits the octave exactly in half (6/12 HS). The name, tritone, comes from when it is spelled an Augmented 4th (see the Pitch Class Interval Quality chart above: F-B, broken down as three whole steps = F-G, G-A, A-B = 3 (whole) tones. In a much earlier system, the tetrachord (4th scale), played an important role in music theory, and “tone” was the common term for what we call a whole step.
You have probably noticed by now that the tritone is not the only interval that can be notated in more than one way. In fact, because of enharmonic spellings, the interval for any two pitches can be written in various ways. A major third could be written as a diminished fourth, for example, or a minor second as an augmented first (practically, though, enharmonic intervals are not that common for beginners). Always classify the interval as it is written; the composer had a reason for writing it that way. That reason sometimes has to do with subtle differences in the way different written notes will be interpreted by performers, but it is mostly a matter of placing the notes correctly in the context of the key (Ch. 4), the chord (Ch. 6), and the harmony (Ch. 8).
Look & Listen!
Any interval can be written in a variety of ways using enharmonic spelling. Play the example above to hear how each pair sounds identical, although spelled differently–explanation below.
- A) In Ch. 2, we called these simply half steps, but distinguish between diatonic (eg., G-Ab) and chromatic (eg., G-G#) spellings. Here, you can see that with the interval number category added, we have to spell them as a 2nd (G-Ab) and as 1st (G-G#),to distinguish the pitch class difference.
- Examples B through D show further examples that are equivalent in sound, but are enharmonic in spelling.
Fun Fact–“wild animal sighting”.
It is possible to even have “doubly” augmented or “doubly” diminished intervals–they do show up in actual music, but rarely. See examples below; the best way to “prove” these to yourself is to look at them on the keyboard, adding in each accidental one step at a time. (Letter D is for you Star Trek fans: the resulting pitch ends up crossing the starting pitch (goes lower)–the space-time continuum has folded in on itself.)
Doubly-Augmented & Diminished Intervals
Doubly-augmented and doubly-diminished interval examples, with their enharmonic equivalents. The number is dictated by the pitch class being used, and the quality is required by the number of half steps.
Inverting Intervals
Knowing how to invert intervals is important for two reasons: 1) it can be used as a shortcut to identify and build intervals; 2) to understand how inversion works with chords (Chapter 6). To invert any interval, simply imagine that one of the notes has moved one octave, so that the higher note has become the lower and vice-versa (this works in both directions!).
Look & Listen!
While inverting, the numbers and the qualities maintain certain pattern, as shown here:
Patterns for Interval Inversion. The numbers always add up to 9, and the Quality patterns are easy to remember: P stays P, the “M’s” swap, and then the “extremes” swap–the largest A and the smallest d.

Concept Check
Example 5-6: What are the inversions of the following intervals?
- Perfect fifth
- Diminished fifth
- Major seventh
- Minor sixth
