Main Body
Musical “Space”
Let’s begin with the piano keyboard because most of us have some familiarity with a piano: no names yet–just a beginning visualization of how music operates [Here’s a useful online piano: https://www.musicca.com/piano. There are also lots of free piano apps for your phone.]
The Piano Keyboard.

The keys (buttons) represent one of the most important concepts of music—pitch—which refers to a label for a distinct musical sound, which could be a letter name, like “D”, or a solfege (which you might know some already) such as “Do” or “Re” or “Fa.” Pitches are like the musical equivalent of colors in a painting; we use them to make up melodies of songs (and several other concepts we’ll learn about).
In physics, Pitch has a mathematical definition, a frequency, that a guitar string or air column (like inside a trumpet) vibrates at. A piano hammer strikes the “A” string and makes it vibrate at 440 times per second (called “hertz”), which makes the air molecules vibrate at the same rate, which then makes our eardrum vibrate at the same rate, and our brain perceives, “A.”
As far as our brain is concerned, psychologists call pitch a “categorical perception,” which is a technical way of saying that our brains like to fit things into boxes so we can process them quickly (this is true of many things, like faces, animals, cars, etc.). When it doesn’t fit the categories that we’re familiar with, it “sticks out” to us, i.e., someone singing “off-key.”
Lecture Video, Pitch:
Range in music refers to a span of pitches; we also qualify ranges in terms of “high” and “low.” We can refer to a person having a high range, that the overall span of pitches that they can sing is relatively high. We can also talk about a song having a high range, that the overall collection of pitches fit in a high range. You can change the effect of range on your car stereo by changing the Treble (high) and Bass (low) controls.
We have a natural sense of high and low already–adults’ voices are lower than children’s voices (particularly before puberty), because the vocal folds of children (the small muscles in your larynx that you use to speak and sing) are much smaller (shorter and thinner) than an adult’s. This is generally true of why men’s voices are often lower than women’s (though not always)–the folds are longer and somewhat thicker. This is an acoustic principle, similar to an instrument string length and thickness; this is also why your voice drops in pitch when you get a cold–the mucus makes the vocal folds thicker, so the pitch is lower (a little gross, but true).
When adults and children sing together (“Happy Birthday,” etc.), they are often not literally singing the same pitch (frequency) when singing the same song, but we don’t consider it to be two different songs, and we naturally handle this range difference without any thought. This range difference is called an Octave Interval and is fundamental to every culture’s music, and is the musician’s term for the distance between two pitches. Joy to the world, is a series of small intervals going down the melody; the ABC song, starts with a leap – a larger interval moving up, then a smaller interval up, then it descends by small intervals.
Back to the piano: on the keyboard, high is to the right, and low is to the left. Try this now on your own keyboard, or right hereat this website: https://www.musicca.com/piano
Try to find pitches that you can sing, and move up and down a key at a time to feel the high and low difference.
This continuum of sound that we use to construct melodies with, is broken up into discrete pitches. Discrete means separate, measurable; this is another way of thinking of categories. You can think of musical space as “sliced up” into pitches that we use to sing and even speak (some languages are very “tonal,” and depend on pitch for meaning).
The piano keyboard is divided, firstly, into groups of black and white keys; this is for visual clarity by providing high contrast. Notice that there is a group of two black keys, then a group of three black keys, repeated. Surrounding these groups are the remaining white keys.
If you count from any key (including all keys, black and white) and then count up (to the right) to that same key (with the same group of surrounding pattern), you will count 12 keys. For example, start on the group of two black keys and count up all the keys–both colors: be sure to include the first key you count, but don’t recount that same key at the end–and you will get 12. Each move from one key to the next is called a step—kind of like walking up a set of stairs.
An example of 12 pitches in an octave.
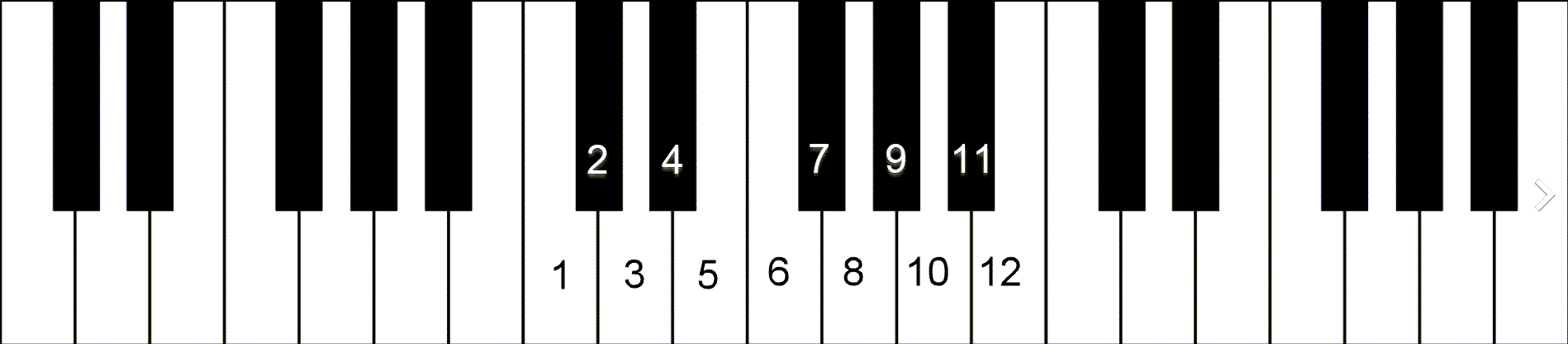
Halfsteps and Wholesteps
Each key (step) on the keyboard–no matter the key color–is called a Halfstep. This is the smallest interval in our system of music. From one key–pitch–to the next (up or down), regardless of color, is a Halfstep Interval. Two HS intervals make a Wholestep Interval (just like a fraction ½ + ½ = 1). Another way to think of it visually is that any two keys with one key in between them make a wholestep. [You might be wondering if there is such a thing as a 1/4 step, or maybe even an 1/8th step? Yes, there are. Quarter steps are actually common throughout music history and today in other world music. Western music used to have 1/4 steps more commonly, but not for some time since equal-tempered tuning (and its precursors) became the standard tuning. This made the ½ step the standard smallest step.]
Examples of Halfsteps (H) and Wholesteps (W) on the keyboard. All of the red dots are a half step apart; the green dots are all a wholestep. Note all the possible combinations of key colors
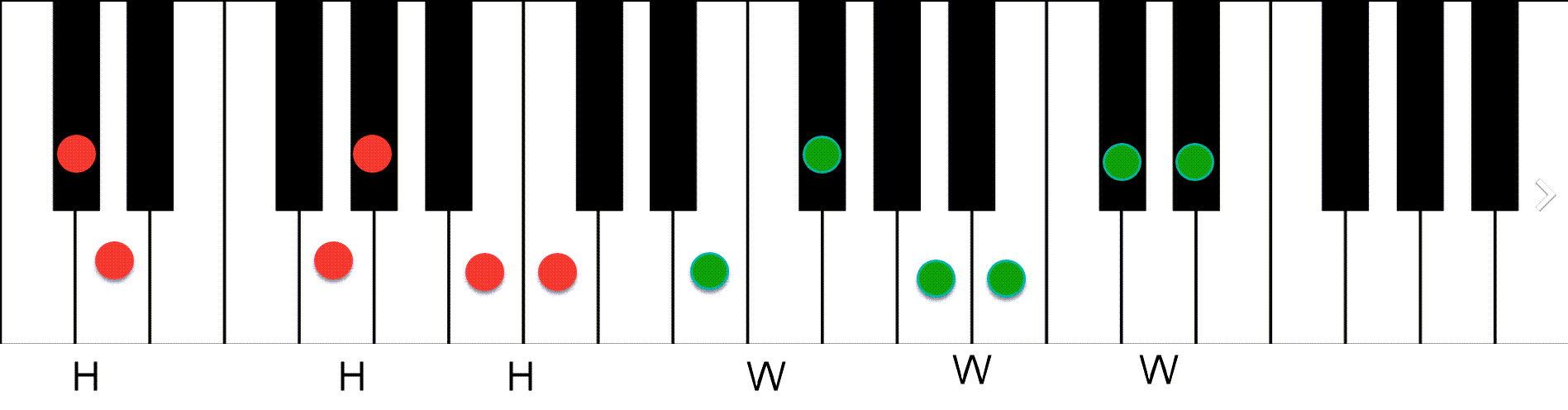
With these two intervals, we can also measure larger distances. For instance, the interval between each pair of circles below is a wholestep plus a halfstep = 1.5 WS.
Marking 1.5 WS on the keyboard. Pitches where there are always two keys in between.

We could measure the interval between any sets of pitches using a combination of HS and WS, but will learn a more efficient technique later. What’s important for now is understanding how pitch is divided and measured, and a sense of high and low within that space. Now, let’s put labels to these pitches, and more precisely define the pitch space.
Pitch Names
Seven letter names (the first 7 of our alphabet) are used to create the basic categories–also called a pitch class–of pitch labels: A B C D E F G. On the piano, these provide the labels for the white keys on the piano, as below.
The piano keyboard with pitch-class labels. There are only seven basic pitch classes that repeat across the range of the pitch space. On the piano keyboard, they establish the key names.

You can also see where the term Octave came from: two of the same pitches are eight pitch names apart.
Lecture Video, Pitch Details:
Lecture Video, Pitch and the Keyboard:
Accidental Pitch Names
We’ve already been using the black keys to create our three intervals of half, whole, and 1.5 steps, but how are those keys labeled? Most simply, they label as alterations of the generic pitch classes. Musicians call these “accidentals,” which is a little confusing because they sound like a mistake–they aren’t. “Accidental” comes from an old Latin word, and the best modern translation is really “alteration.”
As we were creating the half, whole, 1.5 steps, we counted total halfsteps from any starting key, regardless of the key color; however, to reference the pitches we are talking about, we need to use a pitch class label plus an alteration, depending on direction. The importance of this will become more apparent in Chapter 2, when we use all of these pitch concepts on the musical staff, in notation.
For now, let’s go back to the general idea that on the keyboard, moving to the right goes higher and moving to the left goes lower. If I move up by a halfstep, musicians refer to that as going “sharp;” if I move down by a halfstep, we call it going “flat.” You’ve likely experienced this when listening to an amateur singer (think about various renditions of the “Star Spangled Banner” that don’t go too well), and the singer is struggling to stay “on pitch” with the melody–either singing to high or too low. [Note! While this is a case of a musician making a mistake, remember, this is not why accidentals are called that–again, it’s just an old Latin word referring to an alteration.]
The color of keyboard keys has changed over the centuries, depending on the time period and the type of instrument, i.e., the larger keys were black and the smaller were white. Pianos are a relatively late invention (early 1700’s) and harpsichords, organs, etc. had been around for much longer and builders experimented with different arrangements. It’s not entirely clear why, but the main idea is that depending on the material (type of wood), larger, darker natural keys make the contrast harder to detect, especially between E—F, B—C, where there is no altered key. The current arrangement came into favor during the early 1800’s, as the piano grew in popularity, the keyboard size expanded to 88 keys, and the contrast arrangement was considered easier to see.
Psychology 101 Trivia: From a visual perception perspective, the contrast benefit is similar to how reading texts have a white background with the letters black; if this is reversed, the eyes have to dilate to let in more light. For some people, the letters can start to blur and start to “float” which is called halation and happens in about 50% of the population with astigmatism (like me).
Lecture Video, Key Color and History:
Musicians want a way to identify these pitches precisely–and when it’s not a mistake!–so we apply the concept of sharp and flat to specific pitch names, intentionally. Let’s go back to “sharp” and “flat” that we just mentioned. They have symbols to identify them: a flat (moving lower by a halfstep) uses a lower case b and a sharp (moving higher by a halfstep) uses a # sign (it wasn’t originally a # sign, but it’s close enough).
On the keyboard, this means referring to the black keys as an alteration of the generic pitch class, depending on which direction it was altered, as shown here:
Keyboard with enharmonic pitch names. Note that Cb/B# and Fb/E# are fairily rare, but technically correct in certain contexts.
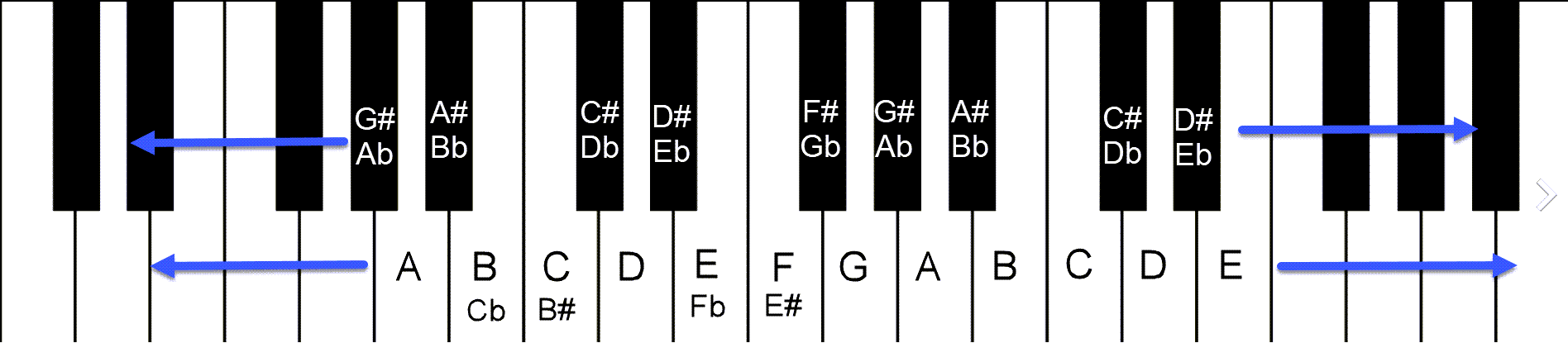
So you can have two different names for the same key on the piano? Yep, that’s right. Since your finger is pushing the same button, why do this? Isn’t that a little confusing? Both good questions. We will look at why more when we do scales in more detail, but for now, the quick answer is it depends on the context. When musicians talk to each other and write music for one another, it can matter how you label and notate pitch names. Think of it this way, analogously: there, their and they’re sound exactly the same, and you don’t know the difference unless you see it written, or understand the difference by hearing it in context. In music, we call this concept of two labels for the same pitch enharmonic.
The Major Pentatonic Scale
Let’s take what we’ve learned so far and apply it to our first scale–-the pentatonic scale—so named because it contains five distinct pitches (scales repeat the first pitch at the octave). All scales are a collection of pitches that follow a specific interval pattern, and the standard way of “spelling” them out is between an octave: starting on a pitch, following the interval pattern, and then ending on the same pitch again. Using our intervals from before, here is the pattern of the Major Pentatonic Scale (we’ll explain “major” soon):
W W 1.5 W 1.5
You can find this on the piano using only black keys, starting with the Gb (red dots), below:
Examples of the Major Pentatonic scale.
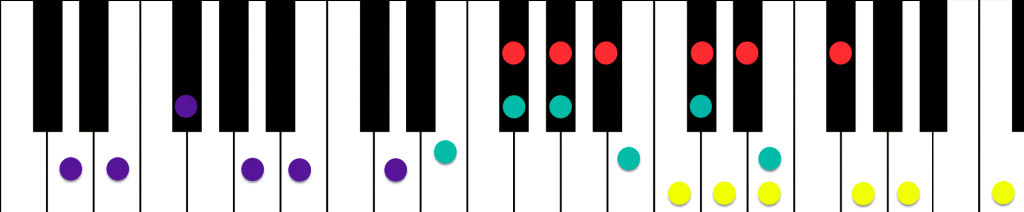
| C Major Pentatonic Scale | Yellow | C D E G A C |
| D Major Pentatonic Scale | Purple | D E F# A B D |
| E Major Pentatonic Scale | Green | E F# G# B C# E |
Play through these on a keyboard (right-click to open a separate window): https://www.musicca.com/piano
Another important point is that you can not (or should not) use just any enharmonic spelling of a pitch in this scale—they should all “match” accidental types for the pitches that need an accidental, i.e., all flats or all sharps. In the scale above, we would call that a Gb pentatonic scale (you could also spell the entire thing as an F# scale). For example:
Enharmonic spelling example of the pentatonic scale.
Gb Pentatonic: Gb Ab Bb Db Eb Gb
F# Pentatonic: F# G# A# C# D# F#
These are played on the piano using the same keys–enharmonically. It would not be correct to spell this scale with the pitch names mixed up:
You need to maintain the same accidental types in a pentatonic scale.
Musicians would find that pretty confusing (irritating, actually), because they have specific expectations about how certain scales work.
This concept is referred to as diatonic versus chromatic spelling. Simply put (there’s more history to it), diatonic means using matching accidentals (called staying “in the key”—more on that later, when we study keys), and chromatic means that you can use enharmonic variants.
Another application of this is how one spells a halfstep—chromatically or diatonically? A chromatic halfstep uses the same pitch-class name—C and C#, and a diatonic halfstep would use a different pitch-class name—C and Db. Therefore, when spelling the Major Pentatonic scale, if you ever use the same pitch class (two of the same letter name), then you’ve made a mistake! Notice in the incorrect example above that there are two A’s.
The major pentatonic scale is the basis of hundreds of songs, so it is very practical to know about. Let’s listen and look at an example that uses the D Major Pentatonic scale. Don’t worry about the “notation” symbols – we’ll get to those in Chapter 2. Just look at the basic contour (shape, flow) of the symbols moving up and down and you listen.
Noteflight – Look & Listen!
Orange boxes denote a Noteflight file, and you will see several of them throughout the chapters. You will also be learning how to use and create with Noteflight yourself!
DIRECTIONS: After you click on the link below: 1) click on the square icon to see this in full screen, if not full already; 2) press the triangle to hear it; 3) press any individual pitches to hear what they sound like; 4) after selecting any pitch, press the triangle to start from that point. Use these directions with ALL Noteflight files.
Look & Listen!
There’s a good chance you’ll recognize this as the very old song folk and gospel song, Amazing Grace. Here’s a list of popular songs that use this scale (https://www.guitarmusictheory.com/major-pentatonic-scale-guitar-songs/).
Enjoy this Bobby McFerrin video where he gives a fun demonstration of the Pentatonic Scale (3:03):
Sing along with this! Also, notice the “steps” and “skips” he puts in that match how you learned to spell the scale.
How does he do that?
- He is using Db Major Pentatonic. First he gives them Db, then Eb, repeats these, then the audience follows him intuitively to F (that’s the “aha” moment when everyone laughs). Then he separately gives them Bb, then they follow him down to Ab, then skips down to F, then all the way up to Db as tonic (the name of the 1st pitch of a scale).
- This works because he begins with the tonic of the Major Pentatonic, and then takes the audience up by WS, which is relatively easy, and mimics 1-3 of this scale.
- After this, he takes them down to Bb – but he has to give it to them. Why? This is the first interval shift, and is one of the 1.5’s in the scale. Once he’s done this, the crowd now “knows” the entire scale and he can go through multiple tunes, even descanting, as he does.
- He does this to show that it’s common to many cultures around the world. In some senses it is, but it’s a little bit of a trick. As I just explained, he had to give them a couple pitches to make the whole thing work, which they would not have gotten on their own. BUT, it’s still a fun demonstration, and partly does shows his point.
